カメラ座標系とワールド座標系の変換

OpenCVのDocumentationにある，ワールド座標系とカメラ座標系の間の変換

(1)\[\begin{split}\begin{bmatrix} x \\ y \\ z \end{bmatrix} = R \begin{bmatrix} X \\ Y \\ Z \end{bmatrix} + \mathbf{t}\end{split}\]

はぱっと見ただけではわかりづらいので，ワールド座標系とカメラ座標系をしっかりと定め，その間の変換(式 (1) )を導出します．

\[\newcommand{\E}{\mathbf{e}}\]

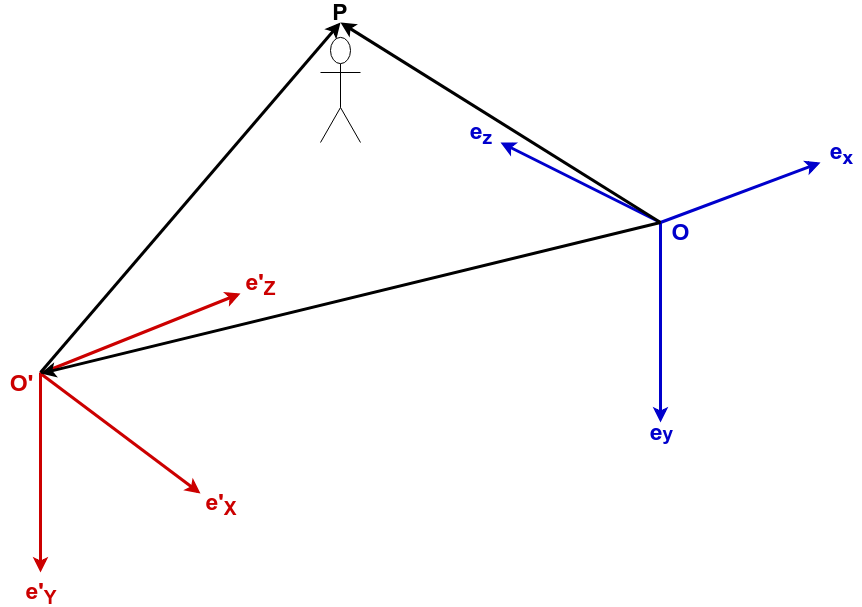
ここでは原点 \(O\) ，基底 \(\E_x\), \(\E_y\), \(\E_z\) から成る直交座標系を \(O[\E_x,\E_y,\E_z]\) と表記することにします．

また，ワールド座標系とカメラ座標系をそれぞれ次のように設定します．

原点を O' としたときのワールド座標系	\(O'[\E'_X, \E'_Y, \E'_Z]\)
位置 O のカメラの座標系	\(O[\E_x, \E_y, \E_z]\)

カメラに映っている物体の座標を P とし，これをそれぞれの座標系で表現すると

\[\begin{split}\begin{align*} \vec{O'P} &= X\E'_X + Y\E'_Y + Z\E'_Z \\ &= \begin{bmatrix} \E'_X & \E'_Y & \E'_Z \end{bmatrix} \begin{bmatrix} X \\ Y \\ Z \end{bmatrix} \\ \vec{OP} &= x\E_x + y\E_y + z\E_z \\ &= \begin{bmatrix} \E_x & \E_y & \E_z \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} \end{align*}\end{split}\]

となります．

ベクトル \(\vec{OO'}\) をカメラ座標系 \(O[\E_x, \E_y, \E_z]\) で表現すると

\[\begin{split}\begin{align*} \vec{OO'} &= t_x \E_x + t_y \E_y + t_z \E_z \\ &= \begin{bmatrix} \E_x & \E_y & \E_z \end{bmatrix} \begin{bmatrix} t_x \\ t_y \\ t_z \end{bmatrix} \end{align*}\end{split}\]

また， \(\vec{OP} = \vec{OO'} + \vec{O'P}\) より，

(2)\[\begin{split}\begin{bmatrix} \E_x & \E_y & \E_z \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} \E'_X & \E'_Y & \E'_Z \end{bmatrix} \begin{bmatrix} X \\ Y \\ Z \end{bmatrix} + \begin{bmatrix} \E_x & \E_y & \E_z \end{bmatrix} \begin{bmatrix} t_x \\ t_y \\ t_z \end{bmatrix}\end{split}\]

と書けます．

ワールド座標系 \(O'[\E'_X, \E'_Y,\E'_Z]\) とカメラ座標系 \(O[\E_x,\E_y,\E_z]\) はそれぞれ別々の座標系ではあるものの，どちらも同じ3次元空間に共存しており，かつ直交座標系であるため，片方の基底を用いてもう片方の基底を表現することができます．

この変換を回転行列 \(R \in \mathbb{R}^{3 \times 3}\) を用いて

\[\begin{bmatrix} \E'_X & \E'_Y & \E'_Z \end{bmatrix} = \begin{bmatrix} \E_x & \E_y & \E_z \end{bmatrix} R\]

と表記すると，式 (2) は

\[\begin{split}\begin{bmatrix} \E_x & \E_y & \E_z \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} \E_x & \E_y & \E_z \end{bmatrix} R \begin{bmatrix} X \\ Y \\ Z \end{bmatrix} + \begin{bmatrix} \E_x & \E_y & \E_z \end{bmatrix} \begin{bmatrix} t_x \\ t_y \\ t_z \end{bmatrix}\end{split}\]

と書き換えることができます．

両辺から基底部分を取り除くと

\[ \begin{align}\begin{aligned}\begin{split} \begin{bmatrix} x \\ y \\ z \end{bmatrix} = R \begin{bmatrix} X \\ Y \\ Z \end{bmatrix} + \begin{bmatrix} t_x \\ t_y \\ t_z \end{bmatrix}\end{split}\\.\end{aligned}\end{align} \]

さらに

\[\begin{split}\mathbf{t} = \begin{bmatrix} t_x \\ t_y \\ t_z \end{bmatrix}\end{split}\]

とおけば，

\[\begin{split}\begin{bmatrix} x \\ y \\ z \end{bmatrix} = R \begin{bmatrix} X \\ Y \\ Z \end{bmatrix} + \mathbf{t}\end{split}\]

というふうに座標変換を記述することができます．